I was working on a longer post about how a pitcher's performance might be affected by the score of the game, or how long the previous half inning took, and I realized that the FIP formula developed by Tom Tango was a bit counter-intuitive to me. I know there are more complex formulas that can perform better, but as a quick predictor of future ERA, FIP seems to be the popular choice. What puzzled me was the use of IP rather than plate appearances (PA) - I thought using IP would bring luck back into the equation, and hence predict lower ERAs for pitchers who happened to have a low BABIP in the preceding season.
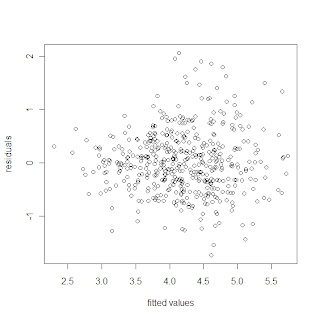
So I did some quick analyses using data from 1995-2008. I fit a weighted (based on IP) multiple linear regression model with season ERA as the response and the previous season's HR/IP, (BB+HBP)/IP, and K/IP as predictors. I limited the analysis to pitchers who had pitched at least 130 innings in both the predictor year and the response year. I'm sure the results wouldn't change much if I didn't use the innings quota, but I wanted to focus on starting pitchers because that's the group my next post will be about. The multiple regression assumptions of homoscedasticity and linearity appear to be reasonable:
The estimates (all highly significant) are:
Rounding off to the nearest integer, my formula agrees with FIP. Then I fit the same model, but with HR/PA, (BB+HBP)/PA, and K/PA (using PA as the weight), and got:
The higher R^2 for the innings pitched model tells us that model does a better job of predicting ERA for the subsequent season. Removing balls in play from the regression equation reduced the quality of the fit, so this is evidence that pitchers do have some control over BABIP.
The data used here were obtained from FanGraphs.


No comments:
Post a Comment